A state machine may be defined in several ways.  
A deterministic finite state machine may be defined mathematically by a quintuple , where:

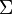• is the input alphabet (a finite, non-empty set of symbols).
• is a finite, non-empty set of states.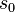
• is an initial state, an element of .
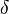• is the state-transition function: .
• is the set of final states, a (possibly empty) subset of .
• (See here)

This is rarefied air far above my head.  But I will use the vocabulary defined here. 

A state machine may also be described as a machine which reads a series of inputs.  When it reads an input it will switch to a different state.  Each state specifies which state to switch to for a given input.  (See here - under the header "Finite State Machine").  A state machine as described here may be used to parse text to determine if it meets a criterion or not.  In this case, the text, made up of text characters as symbols, is supplied to the state machine, which operates until it reaches one of the final states indicating the outcome of the parsing.

A state machine may be described as event driven if the alphabet consists of symbols representing outside events, and entering a state triggers a state function to produce some response to that event.  Typically, data associated with the event is supplied to the state function, and the state function produces output data in response.  Such event-driven state machines are often implemented as threads or processes communicating with one another as part of a larger application. For example, a telecommunication protocol is, most of the time, implemented as an event-driven finite-state machine.  (See here).